Teaching and Learning – Teach Solutions

Finish Strong

This blog gives advice for all the things teachers should and should not be doing in that run up to exam season

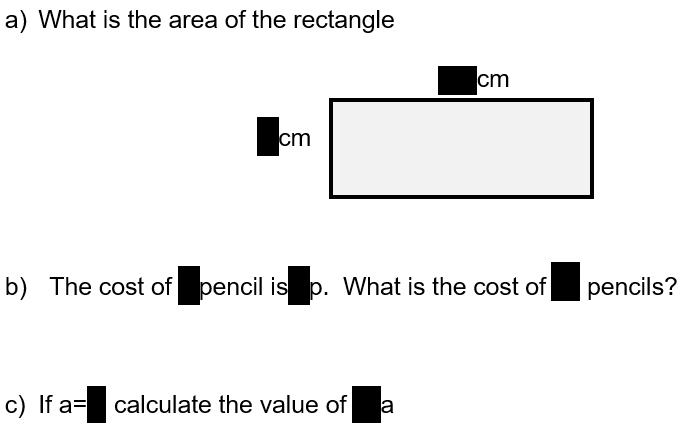
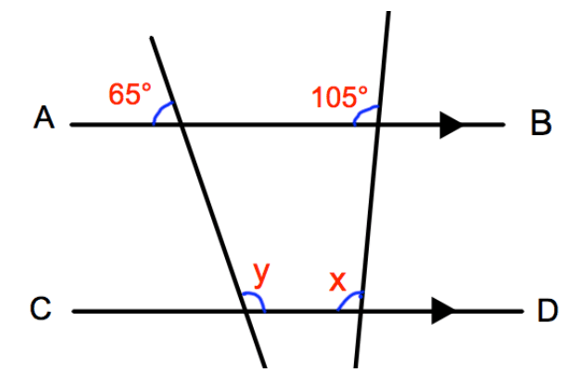
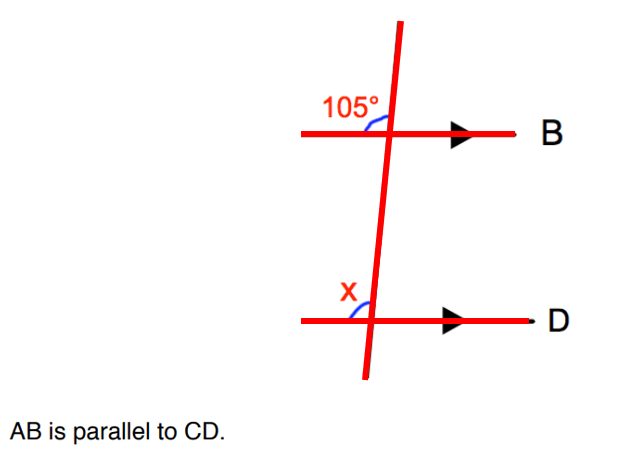
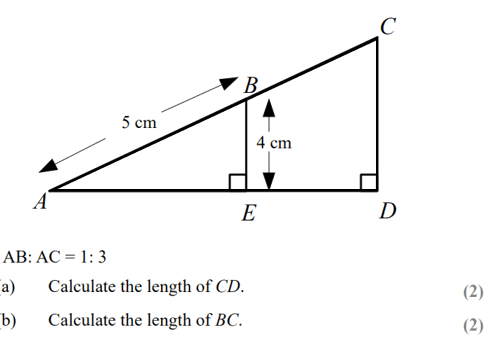
A while ago I wrote a blog aimed at giving tips on how to start strong with a new class at the start of a year, it’s here and was called “Starting Strong”. As the countdown to exams have started it felt right to close the loop with this one.

Here are some dos and don’ts for working with pupils as their exams beckon. I am going to focus this around Y11 Maths in England but I suspect it wouldn’t take too much work for someone to decide what parts would apply to them with a different subject/country/age-group.

Let’s start with 7 “don’ts”. These are things I see often enough that they warrant a warning sticker.

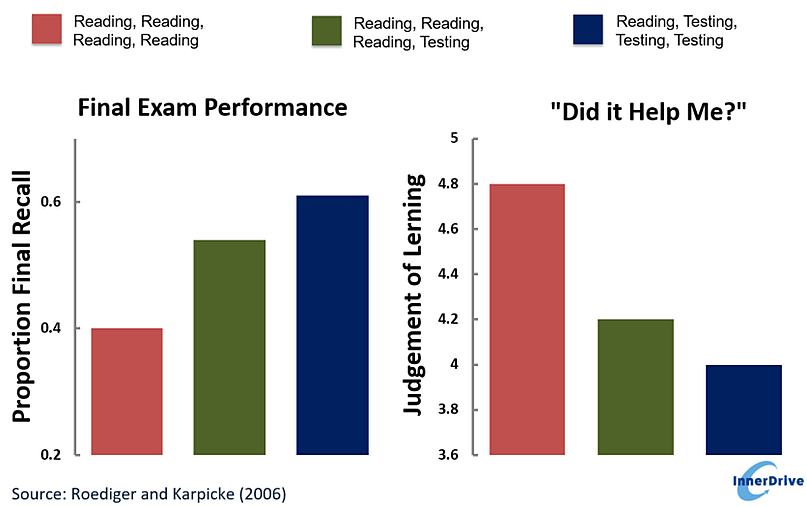
Don’t make them sit paper after paper

It’s important to remember that students aren’t going to start learning any differently just because exams are nearer. Don’t put one lesson a week aside for them to complete an exam paper if you haven’t had time to address all the major gaps in their learning from the last one. This is a form of “means end conflation” but getting them to sit lots of papers is not necessarily going to make them any better at completing them.

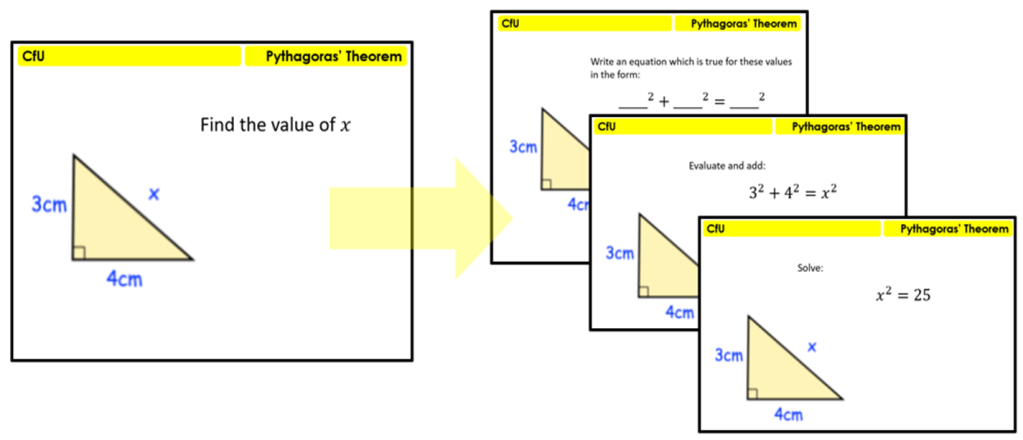
Don’t review papers by going through them one question at a time

If students have completed a paper, it isn’t a good use of their time to simply see the teacher go through it on a visualiser whilst they self-assess. If the pupil has got a question correct, they learn nothing. If they got it wrong, they need some teaching and purposeful practice on whatever the concept is. If students learnt an idea by simply seeing a teacher complete one very specific example one time and then moving on straight away, teaching would be a very easy profession.

Don’t intervene by grade

Don’t make intervention groups purely based on grade. Identify key areas of curriculum weakness and group them by these where possible.

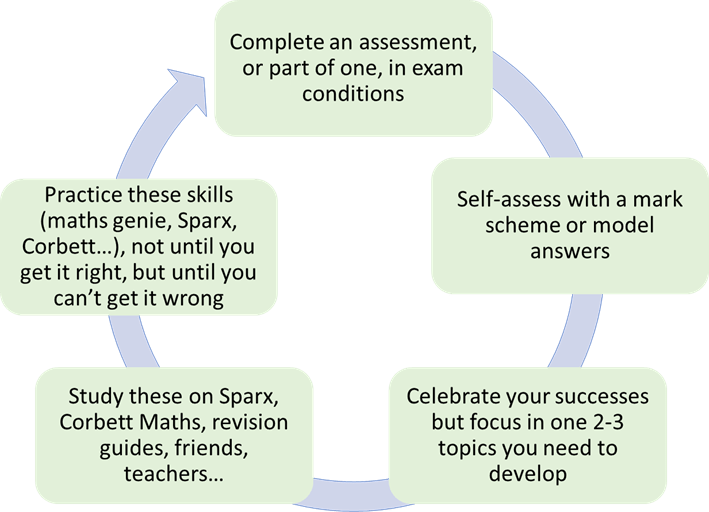
Don’t assume students know how to revise

Don’t set homework of just “revise” unless you have explicitly taught them how to do this. Even then, be as specific as you can.

Don’t overload them with resources

It isn’t helpful to give them 2 revision guides, 6 exam papers, 10 knowledge organisers, and 3 websites to use. Yes, you will give students all the tools they may need but this is overwhelming and lacks accountability. Keep things tight and achievable. Find one or two great resources and invest in these. Less is more.

Don’t try and cover everything

It isn’t ideal to cover every aspect of the curriculum if it means a large part of it won’t be learnt well. Making the hard decision to cut content, but learn fewer things well, can lead to students performing better in their final exam.

Don’t think you’ve ever “completed” the curriculum

This one is just a little bugbear but I often hear the phrase that a certain class has “completed/finished the curriculum”. I then look at data and they aren’t all achieving 100%. It makes me wonder in what sense the curriculum has been completed. It would be equivalent to painting a patchy first coat of paint on a wall and saying, well, I’ve covered the whole wall so I’m lost for what to do next. The curriculum is not a thing to be completed, it’s a thing to be taught, studied and learnt.

Let’s move on to some “dos” then. Some of these are a cheat because they are the opposite of some above but, it still counts. Most link to bigger ideas in blogs I’ve written previously. Check any out that you may be unfamiliar with.

Focus on exam technique

Knowing the course content is one thing, but there will be advice you can give which is specific to the way the exam is assessed or written. I think, in maths, the difference between two students with equal maths knowledge but with opposite exam techniques can easily be a grade. See here for how to get more marks on a maths paper without knowing any more maths.

Use QLAs effectively

Instead of going through an exam paper from front to back, use QLAs wisely. Advise on that here.

Share your plans with the students

When you’ve created your plan for your final run of lessons, share this with pupils. That knowledge, combined with them having ownership of their own most up to date QLAs will let them know the small subset of topics that they will need to revise independently because it won’t be covered with everybody in class.

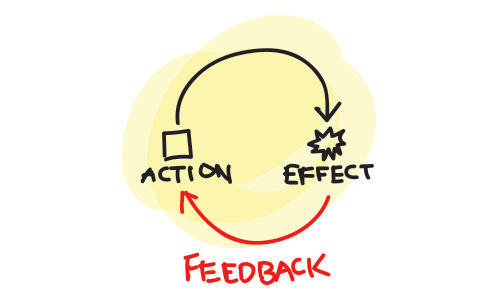
Feedback effectively to assessments

I wrote in the “don’ts” the ways you shouldn’t feedback to an exam, here’s how to do it well.

Teach them how to revise

Revision is hard and effective revision can sometimes be counter intuitive. Teach them how to revise. For more on that, see this blog.

The Main Point

It is so tempting to feel the need to drastically change things up as exam seasons gets closer and closer. It is your job, ultimately, to still teach students how to do things they cannot do. This has been your job all through the year with every year group you teach. Hold fast and carry on doing the same thing. Keep the balance of modelling and practice. Keep the balance of checks for understanding and responsive teaching. The only thing I can see a good argument for changing is the ratio of time spent retrieving content, simply because by this point there is so much more to retrieve. It can be hard to resist the urge to change things up but if you believe you’ve been doing a good job for students the rest of the year, there is nothing special that needs to happen. Hold fast. Stay the course. You got this!

Rethinking Results Day: A Guide for School Improvement

We’re used to thinking about winners are losers, and this summer of sport has been no different. But how can this lens be a used productively when thinking about results day?

As the Euros blurred into Wimbledon which in turn blurred into the Olympics, a summer of sport is soon going to take a hiatus for the most important competition of the year; results days. Whilst the rest have very clear definitions of what winning looks like, results day does not.

This is an incredibly fitting reference for this blog but is also very niche (2 points if you got it)

It’s likely your school will have numerical targets that have been set which may or may not end up being met… but there are no winners, not officially. Some schools will top league tables for various metrics but there are over 3,400 schools in England so does this mean there will be a handful of winners and a hell of a lot of losers. That doesn’t seem right though, not when so many schools are working hard, doing the right thing, and making good progress. It’s time to rethink how schools interpret results day. Let’s do that through answering a series of questions.

Here are the questions:

Is competition OK?
How should results be analysed through the lens of school improvement?
How much improvement is enough?

Is competition OK?

100% it is. Teachers are some of the most consistently competitive people I’ve ever met. Competition is no bad thing and, when gone about the right way, can be a powerful and useful leverage. Just be very careful who you get into competition with. There are some amazing schools out there and some of those will likely have a similar demographic to you. There are state schools delivering transformational educations in inner city, rural locations, coastal settings… using these, especially those in a similar situation to yourself, for inspiration makes perfect sense, but for competition does not.

The only school I think is worthwhile any school being in competition with is itself. Schools leaders inherit schools in various states and the only requirement on them should be to try and work towards improving the school at the quickest rate they can whilst remaining sustainable in the long run. Competing with an established school that has been doing this longer than you, is like trying to win a race against an Olympic athlete who already has a head start.

In some years this might mean an increase in exam results is expected, in others, if there have been massive staff shortages, local troubles, finance issues, strikes… then even maintaining results could be considered a win. Context is king here.

How should results be analysed through the lens of school improvement?

The short answer to this is: CAREFULLY!

Let’s say you’ve visited a school that you love. It’s results are amazing, it’s staff and students are happy. It’s everything you ever wanted to create. Let’s then say that you spent last year building that in your school and it was a success. If all that has happened then your results that year still aren’t even going to be close to emulating the results of the other. Results are the slowest thing to be affected by school improvement initiatives. Why is this? Simply it’s because results aren’t the result of the current state of the school but the culmination of a learner’s entire journey through it. No matter how good a student’s Year 11 experience is, no matter how much intervention you threw at them, how much you spent on residentials, nothing even comes close to the power of 5 years of consistently high-quality teaching.

This means new initiatives should not be abandoned just because they appear ineffective in the short term. A sensible follow-up question this does raise is how do you know if something IS working?

Well, the safest thing to do here is not to innovate but to personalise. We know enough about what works to know that if you are leading in a school or department sitting outside the top 5% performing then it shouldn’t be your job or responsibility to invent something. It should instead be to implement something which has been proven to work elsewhere in a similar setting. This still will require levels of personalisation as, no matter how closely aligned to your setting it is that you can find a great school, yours will be unique and strategies will need adapting. You need to focus on the active ingredients of what made it work for the other school. (For an example of this when it comes to the effective teaching and learning, check out the T&L Framework here: https://teachsolutions.uk/files-and-documents/).

There is too often a need in education for people to reinvent the wheel, to discover some new silver bullet, to innovate. In education, you don’t need a USP, you don’t need to compete with the market in the same way that Samsung and Apple do, you can shamelessly copy what works without fear of being sued, so do it! Take the 90% of the active ingredients that make great schools great and use them. Just be careful not to visit a school and then only take the easy superficial stuff (for more on that idea, read this https://teachsolutions.uk/2023/07/18/buying-coconut-oil-didnt-give-me-a-six-pack/).

Too often also, school initiatives belong to individuals, rather than to the school. School’s policies, visions, systems… should reign supreme here. Anything major that a leader starts, should be approved from their line manager with careful thought about how this work can, if successful, be continued when the leader leaves the building. What documentation exists? What writing exists? Senior leaders tend to stay in schools from between 4-7 years. That is just over 1 full cohort of Y7-11 going through. To ensure that the school doesn’t have to start again from scratch but that systems can be tweaked, rather than created anew, structures (and not just temporary scaffolding) need to exist which ensure the school can continue to move from strength to strength.

How much improvement is enough?

If we change what winning looks like to thinking about improvement, year-on-year, a very reasonable question is “how much progress is enough?”. This is a tricky one. At this point I can only comment on what I have seen and lead on myself. As a head of department in a school with supportive systems, a fully staffed department (though with our fair share of ECTs), we managed a consistent 0.45 progress increase year on year from 0 when I took over to 1.8 the year after I left. That is a target I informally set heads of department to make (whilst appreciating there are lots of mitigating circumstances that might make it not possible). Whatever other metrics you might have in place, at the end of day, there should be a real impact on the children being served and, although it might not be how we would always want them to be judged, the outside world treat exam results as a keys where the higher the results are, the more doors you can open. Until that changes, exam results are crucial when judging our impact as educators.

The big day

When the day comes then, take time to celebrate successes, to congratulate colleagues, to spend time celebrating with proud students and their families and consoling/coaching those who are less happy. Then, when it comes to doing the analysis, be sure to not look around the country and your local area so much but look at your past self. When drawing up or editing school improvement plans, don’t throw everything away if you’re not happy, remember that change, real change, takes time.

Independent Feedback Loops

The content discusses the impact of immediate feedback on learning. It highlights the importance of independent feedback loops in subjects and suggests strategies for creating effective feedback in different learning scenarios.

Imagine you are at a carnival. There is a target you need to hit with a bow and arrow. There is also a blindfold which you have to wear. The person running the stand shows you where to aim and models themselves doing it perfectly and hits the bullseye. Now it’s your turn. You have 10 attempts. You also have the choice between two different scenarios you can choose between.

Scenario A – You can remove your blindfold after each attempt to see how close the last shot was.

Scenario B – You have to wait until all 10 of your attempts are up before removing the blindfold.

Which scenario is going to yield the better result? Undeniably, it’s going to be A. This is despite both involving the exact same modelling and equal opportunities to practise. It’s because A has the advantage over B in allowing you to adjust your practice based on the near-instant and ongoing feedback.

Let’s call scenario A an “independent feedback loop”. This is where the user receives feedback which they can act upon instantly with no direct input from another expert needed, and now let’s move this into the classroom. How do independent feedback loops play out at school.

Some subjects lend themselves naturally to these loops. When teaching a serve in tennis, certain techniques in art, music, DT…. The practical subjects where there is a clear model of excellence and the user can see instantly the difference between what they are producing and what they should be producing. Compare this to completing a set of maths questions, analysing an historical source or writing a piece of fiction and suddenly the benefits of an independent feedback loop disappear. The question of this piece is, for situations like those just mentioned, can an independent feedback loop be created and, if not, what’s the closest we can get to simulating one?

Let’s start off with a maths example. Scenario B would translate as students working away at 10 questions and then, once they are all done, the teacher shows the answer to the class and they find out how they have performed. Some might find out they have got everything wrong, some only parts and others might be relieved to get 10/10. For those who got some or most wrong, their time spent practising at best was a waste and at worst has helped embed some misconceptions which might move learning backwards for them. Now, if a lesson does get to this point, the teacher would have a variety of options open to them, but this article is exploring if anything could have been done during the practise phase of the lesson.

Subjects where there is a pre-determined correct response.

1. Don’t wait until the end to share the answers: When questions involve multiple steps and there is no way that students could just pluck the answer out of thin air, there is no harm in sharing answers alongside the questions straight away. The usual safeguard of protecting against copying is not needed since the working out is what will hold them accountable. If questions can be solved with no need to show working out, then having an “answer bank” which has all the answers but in a random order displayed, can achieve a similar effect whilst maintaining high levels of accountability. What this won’t do is tell the students where they went wrong. It might encourage them to check their work and they may be able to self-correct. At the very least though, they will know they need some help before continuing.

2. Combine the above with backwards faded examples: If the problems require multiple steps to complete then, by using backwards faded examples which add an extra step as the questions develop, combined with answers being shared, leaners will be able to pinpoint the exact step at which they have a gap in their learning. That knowledge combined with clear notes or examples, should help them self-correct. The worst-case scenario here is that the student knows specifically what they can’t do but is unsure on how to correct it.

3. Build self-checking mechanisms explicitly into the task: If it’s possible to equip learners with the skills to check their own work, that would be ideal. In certain questions where answers can be self-checked with substitution or some other process, teachers should make it an explicit part of the task that is being completed. Instead of the question only saying “solve this…”, including a part which says “using substitution, check your answer”. Estimating answers beforehand can also be a useful tip.

Again, do not rely on learners doing this themselves, adding in an initial part as “estimate your answer to the question” before asking them to solve it, will help encourage these behaviours. Estimating and checking are both things learners are often asked to do implicitly but without making it an explicit part of the question it will not happen and never become a habit. Too often students will do the minimum required of them so if the wording in the question (the ultimate source of authority here) doesn’t ask for something, it is less likely to happen.

Subjects where there is no one right answer and also no in-built independent feedback loop

1. Clear and sequenced success criteria: Giving learners explicit success criteria to hit at specific points can help them self-assess their work. Giving a physical checklist containing targets like “in paragraph 1 make sure you include…” or “in your final paragraph make sure you refer back to…” can help learners assess and improve their work as they move through it. Where the success criteria is less pinned to a specific part of their work, a checklist can do the same thing. Asking learners, after an allotted amount of time, to highlight in their work where they have hit the criteria that they are aiming for can help them reflect and improve.

2. Share examples and non-examples before the end: Pausing learners and sharing some great exemplars and some misconceptions can also help learners reflect on their own work. Again, it’s important this is done before the end of their allotted practice time. When doing this it is important that the teacher ensures everyone understands the underlying properties that make the work being shared good or bad. Everyone’s work will be different and it’s important that the essence of what makes it great or not is discussed, beyond just the superficial content of the work.

Summary

Teachers can do a lot before independent work starts to check learners are as ready as possible and they can do a lot after independent work finishes to rectify any mistakes that have emerged. Let us not forget that there is also plenty that can be done, through careful thought and task design, to ensure that time spent practising is always time well spent.

I’m always interested in what people make of this so please feel free to comment with thoughts, questions or incomplete musings. Follow this or my Twitter account Teach_Solutions for similar content in the future. Also, check out the rest of this site, there’s some good stuff knocking about the place.

Do You Know Where Your Holes Are?

Ever wondered why ancient buildings are so beautiful and strong that not only are they are still around today, but they can also still create such awe and wonder? “We don’t make ‘em like we used to”, hey. To find out why this is the case, we will travel back to WWII.

When planes were sent over in the war effort their damage was analysed upon their return. This was to see where reinforcement should be placed in order to better protect them from enemy fire.

Analysis of all the places planes are being shot at, like in the image on the left, would let engineers know where to add extra armour. The aim here was to ensure more planes returned home than previously. Armour was added to the red areas, since this is where the data suggested the enemy guns were hitting, and planes were sent out again. Unfortunately, it had little impact.

Enter Abraham Wald. He was a Jewish Hungarian, who, when antisemitism rose in Europe, moved to America. When the war broke out, he was at hand to aid to Allied effort. Like so many unsung heroes of WWII, he was a mathematician. He said that if we only look at the bullet holes of the planes that have survived then we are leaving out a crucial set of data, those that did not.

Whilst it would be impractical to go and find the planes that had been shot down, perhaps we could infer this information from the survivors. If we look again at the image of the plane and realise that these are the bullet patterns of the planes that have returned, it suddenly isn’t a big leap to say that the armour should go where the red dots aren’t. It is likely the planes are being shot everywhere but, since we can’t see any planes that have been shot in certain areas, this is more likely due to shots there being devastating to the plane, rather than that area being missed.

This is an example of survivorship bias – only looking at the data of those that have “survived” to inform your decisions. This is also the reason why it can appear that all ancient buildings are strong and awe-inspiring; the reality is those that weren’t have either collapsed because they weren’t sturdy or have been demolished because they weren’t impressive. There is little choice but for the ancient buildings that are around today to be strong and beautiful, they wouldn’t be here otherwise.

What does this have to do with education?

It is not uncommon to see in the public domain, people deriding the use of explicit methods of teaching. Phonics and fronted adverbials are common targets here.

An author (as all the people above are), criticising how reading is taught in schools is another example of survivorship bias. They think that, understandably, they managed to flourish without needing these methods so therefore it isn’t needed for anybody. What they are omitting from their data is the thousands of pupils (more likely than not, disadvantaged pupils) who left the education system the same year as them with little to no literacy. This explicit teaching is not for the few who survived, it is for those who otherwise wouldn’t.

“Since the introduction of the phonics screening check in 2012, the percentage of Year 1 pupils meeting the expected standard in reading has risen from 58% to 82%, with 92% of children achieving this standard by Year 2.” DfE

What about teachers? Do we carry this bias around with us and how might it present itself? If you’re teaching in a school the chances are you have a degree, for that, you probably did pretty well at school. Whatever your background, you most likely found ways to navigate the system. This can lead to assumptions about all learners. It can lead to assuming that others don’t need certain structures put in place because you survived without them. It can lead to people deriding, not explicit ways of teaching vocabulary, but explicit ways of teaching anything.

If you’ve successfully navigated school and are now a teacher, you might ask:

Why do I need to explicitly teach learners how to revise?

Why do I need to teach self-regulation?

Why do I need to use routines in my lesson?

…after all, I survived without them.

If you’ve successfully navigated being a teacher, and are now leading teacher in some way you might ask:

Why do we need these frameworks and policies?

Why do I need to show others how to explicitly teach/plan?

Why do I need to share my tips for teaching?

Why do I need to line manage people so explicitly?

…after all, I survived without them.

It’s important when systemising processes and making things more explicit that we do not take agency away from individuals and that our plan, in the long run, is for them to be successful independently of us. Our aim is to produce a cohort of staff and students who don’t just survive but thrive in the education system. To do this though, we need to look beyond the success stories, the top sets, the high fliers, and think about those that might be struggling and what extra armour needs putting in place to ensure they succeed too. After all, a bit of extra protection, if you don’t need it, does no harm.

Summary

It is important to know that in many ways, you are a survivor. This is something to be celebrated but also something to be acutely aware of. As a teacher, you likely need to give many students more explicit help then you ever received yourself. As a leader, you likely need to give many teachers more explicit help than you ever received yourself. Remember, this isn’t for those people who are going to be fine otherwise (though they are likely to benefit too), it is to ensure that no matter what, when you work or learn at a great school, you have just as much chance of succeeding as anybody else. In short, make sure you know where your holes are, or perhaps more aptly, where they aren’t.

Teaching Mixed Attainment Maths at KS3

Advice on how mixed attainment maths at KS3 can work

I am both a big advocate for and against mixed attainment maths teaching at Key Stage 3. When done right I believe it is better both academically and ethically for the children. I know it can work, I’ve seen it work, I’ve been the Head of Department of a school that taught mixed attainment maths in KS3 and got some of the highest progress scores in the country. I have no doubt it can lead to incredible outcomes. The difficulty comes in “doing it right”. It takes A LOT to do this. And the risk of not getting it right I believe is greater than when teaching more homogenous groups. It’s a high risk high reward strategy.

What worries me is that people may make the ideological choice to move to mixed attainment teaching, or they may do so for some other logistical reason (staffing, timetabling…), and although it may be worthwhile in the long run, if it isn’t implemented right in the short-term it can be detrimental to all involved. Staff can be overworked when suddenly shifting to a whole new pedagogical approach and students end up receiving a worse education than they were originally. In the worst cases this is not only done without consulting the maths team, it is done against their own desires. Whilst it might be OK in a few years, there is an initial cohort of both teachers and learners who suffer needlessly in the immediacy.

Maths is innately more hierarchical than most other subjects and the decision to teach it in mixed attainment groups must be deeply considered by school leaders.

Below I want to go through some of the key principles that I have seen and used that have made it work in practice. These often are not things which can be implemented overnight.

The key points I’m going to speak on are:

The curriculum
Early intervention
Atomisation
The well-worn path
Effort over attainment
Means of mass participation
Explicit instruction

Curriculum – A rising tide lifts all ships

One of the biggest issue in mixed attainment maths teaching is students not having the pre-requisite knowledge to engage meaningfully in things their peers can. The department should still endeavour to teach the entirety of the KS3 curriculum but this needs to be done over 3 years. They should ensure that none of the topics that sometimes “leak” into Y7-9 from KS4 appear (factorising quadratics, solving simultaneous equations algebraically, index laws…). The scheme of work needs to go back to basics and build up slowly. It should start with numeracy and the basics need securing and mastering.

There are plenty of rich activities which can be used to both challenge students whilst helping others practice. If some students need “stretching” then exercises should go deeper rather than broader with the key concepts being taught. It is impossible to perfectly cater for all students all the time.

Teachers should be secure in the knowledge that, over 5 years, students will encounter all the content they need to get 100% in their GCSEs. They shouldn’t worry about holding a few students back in the short term for the betterment of all in the long run. Holding some students back to ensure all can access the content is better than the converse of letting some fly whilst others never master the basics. My second in department used to routinely remind me that “a rising tide lifts all ships”.

Early intervention – Build on solid foundations

Linked to the above, if there are students who join you in Y7 who cannot access the beginning of your course due to weak numeracy then you need to intervene. This should be a relatively small number of pupils. The culture around intervention needs to shift from happening at the end of Y11 to the start of Y7. Intervene early. Either employ or upskill staff on the teaching of Ks1-2 maths and put all the effort you would put into Y11 in the run up to their GCSEs into identifying and addressing serious gaps at the start of Y7.

This is the strategy that all schools should be using anyway, since if you sort the basics out then students will spend the rest of their time on the course building on solid foundations.

Atomisation – Break it down and build it up

Before teaching any new concepts teachers should go through a rigorous process of “atomisation”. Of breaking the concept down into the component parts that make it up. They should go through the list and decide what they can safely assume students know, what is essential to master this new concept, and what might be a “nice to have”. All of the essentials should be checked or reintroduced in the lesson prior to teaching the new content.

When it comes to teachers deciding what students may already know it is always better to underestimate than overestimate. If you underestimate then you only risk wasting a minute or two whilst you check for understanding and realise students can do it. If you overestimate, you risk tying yourself in knots later in the lesson and having students leave without grasping a thing. Whatever new concept you are teaching, break it down and build it up.

Well-worn path – Visit everyone but do not give them all your time equally

Do a well-worn path; this is a technique to be used whilst students are working independently. It involves mapping out a route around the classroom in which you can have eyes on every student’s work. As well as using it to check all necessary accessibility arrangements are in place (glasses, readers, dictionaries…) you can use it to check everyone’s work. It is worth starting a lap visiting your highest attainers first. These are a good proxy for any serious misunderstandings since if they are stuck it is likely everybody is and you can bring everyone back together. It is worth ending your lap with those who often require the most help. This is so that you can help them AFTER you’ve briefly touched base with everyone else.

It is OK to spend more time with some students than others. It is also OK, if there is a TA, for them to not always work with those who need the most help as the teacher may be better placed to intervene effectively. We are not aiming for equality but for equity. That involves visiting everyone but not giving your time equally.

Classroom culture – Praise effort over attainment

Maths undeniably has a PR problem. Some (most?) students will, by the time they start in Y7, already have a pre-conceived idea of how much they can achieve in maths. It’s important to build a culture where all students believe in themselves, perhaps more so in a mixed attainment setting where some will be doing maths alongside peers who are much more confident than themselves.

Take the time to praise the right behaviours that students exhibit. The peak-end rule suggests that what happens at the end of the lesson will really stick with students. To leverage this, end on something attainable, you shouldn’t be finishing your lessons with the hardest content. Treat your lesson like an exercise class and end with a warm down, not a sweat-fest. Make sure they leave feeling successful. Catch those most vulnerable doing good early on the lesson and make them feel great. In every interaction ensure that you are praising effort over attainment.

The final two are kind of cheats because they don’t apply specifically to mixed attainment maths teaching, I think they just apply to all teaching, but it can often be the case that people don’t think they do apply in this setting so I just wanted to make the point that they most certainly have a place.

Means of mass participation – who cares if less is in their books if more is in their heads

You need to have a system set up in the lesson to ensure that, as much as possible, everyone is ACTIVELY participating for as much of the lesson as they can. Mini whiteboards are the obvious (and best I’ve seen so far) solution to this. When checking pre-requisite knowledge, why ask one student when you can ask everyone? This is especially important in a less homogenous group where gaps and misconceptions can be harder to predict.

When it comes to students working in books it is nearly impossible to see everything that is happening. If more questions than usual are completed together (but still independently) on mini whiteboards then the teacher can be sure that if the need arises for students to work in books or on a sheet or something that they will be able to do so without embedding any misconceptions or being stuck. Remember that practice doesn’t make perfect, it makes permanent. Also remember that it shouldn’t matter if there is less in their books at the end of a lesson if there is more in their heads.

Explicit instruction – all the principles of effective teaching still apply

A common misconception that I see is the idea that mixed attainment teaching is not compatible with explicit instruction. This is far from the truth. It can be tempting to think that with so many different starting points in the room tasks need to be really open or many tasks need to be available. This simply isn’t the case.

When mixed attainment teaching either hasn’t been very effective for a few years or starts at once in Y8 or Y9 it’s easy to see how this conclusion is reached. With all of the above in place though, you can start from the ground and build up remembering that all the principles of effective teaching still apply.

Things to definitely avoid

As well as doing all of the above, here are some brief “do nots”:

Do not start mixed attainment teaching at KS3 all at once, begin at Y7 and build it up
Do not start it and THEN put the CPD in place, get the CPD sorted first then make the switch
Do not do this TO the maths department, do it WITH them

The end and the future?

I sincerely hope that mixed attainment maths becomes the norm in the future but this is not a change that can happen quickly and I fear that we are putting more and more staff off it at the moment due to poor implementation. If the above ends up being of any use, I’ll be a happy man.

Beware the Ends of Branches

This post looks at certain topics which are often neglected when it comes to retrieval, why that happens, and what can be done about it.

Let’s start with a quick question. What seemingly accessible topics in your subject do students never seem to be able to remember?

In my subject, this is an easy one. Ask any maths teacher and their list will most likely include:

Loci
Constructions
Congruency
Simultaneous Equations
Cumulative Frequency Graphs
Averages from a table

Retrieval

Retrieval, retrieval, retrieval. It is a necessary part of learning (remembering?). Learning, not just performing, does not happen when something is seen once and then never again. You need introducing to something, you need to almost forget it, then you need to rescue it from your mind before it fades away just in time to keep it in your head for that little while longer.

In mathematics, some topics are naturally retrieved. With no effort from the teacher they will recur again and again. If we take solving two-step equations as an example, once taught as a discrete topic, it will rear it’s cheeky head when students move onto:

Forming and solving equations
More complex linear equations e.g. three step or with unknowns on both sides
Simultaneous equations
Quadratic equations
…

If we take basic angle facts, these will reappear when moving onto:

Angles in parallel lines
Forming and solving equations
Certain ratio problems
Angles in polygons
Circle theorems
Bearings
…

Why does this matter?

Retrieval, retrieval, retrieval. It’s just so important in embedding content, it means that the ideas above that recur are more likely to be learnt (remembered?).

A Curriculum Tree

If we imagine a tree of maths knowledge representing a curriculum. In this tree, the core ideas which appear everywhere form part of the sturdy trunk. Let’s imagine branches grow from pre-requisite materials, these more fundamental ideas mentioned above would form some of the more solid parts which would have many offshoots. As we track any branch to its end, you would find a topic that is not needed for any other topic for that curriculum.

The closer a topic is to the trunk the more naturally it will be retrieved. The topics at the end of the branches, however, are not going to naturally be retrieved whilst going through a curriculum. This is a problem. Why? Because retrieval, retrieval, retrieval, is so important to remembering (learning?).

Ends of the Branch

Because of how important retrieval, retrieval, retrieval is to learning (remembering?) we need to pay special attention to the ends of the branches. These will not recur naturally so we must find ways to force them into the curriculum. Most schools in the UK these days achieve this at the start of the lesson with some sort of retrieval activity. I think this is a great idea. Without revisiting content regularly there is a risk of it not being remembered and the start of the lessons seems a better place than most in which to do this.

It follows (if you believe all of the above) that the topics at the ends of the branch need special care and attention when designing these retrieval tasks. Beware the end of branches!

This all seems simple enough. Problem solved, right? Well, hold up a second.

There are some topics that, for various reasons, just complicate things.

I see hundreds of lessons a year and am yet to see a retrieval starter in which students need to recall loci or constructions, and very few where they retrieve cumulative frequency graphs, averages from a table or simultaneous equations etc. Does that list look familiar? (Don’t worry if you’ve forgotten it, we haven’t retrieved it yet), but it’s the list that we started this post with.

There is an uncanny crossover between what I do not see retrieved and the seemingly accessible topics that teachers will proport students struggle to remember. Could it be that it’s because students are not asked to retrieve this content as often? I would say so.

It’s perfectly understandable that this happens though. Nobody wants to spend the beginning of their lesson retrieving loci or constructions because it will inevitably lead to chaos as students do not have the necessary equipment.

Cumulative frequency graphs and averages from a table questions will require printing which is logistical barrier.

Simultaneous equations and congruency questions often require so much writing they may not fit into a snappy 5-minute starter routine your school so heavily insists on.

Solutions

If you or your department uses starts of lessons in this way then please beware the ends of branches. Not all of them, but those which require that little extra consideration. These can be easy wins but without putting in that extra effort every now and then to ensure students retrieve these topics, they are doomed to be forgotten (not learnt?).

Remember:

Take time to mark out explicitly when teachers should be reviewing these
Have some pre-prepared printable sheets ready
Have a class-set of equipment on standby for certain weeks
Be ready to (justifiably) take that little bit longer on the starter

Without taking special care, some branches will never be able to blossom.

Teach Them HOW To Revise

A summary of revision tips for teachers to use with students.

In the run up to exams students should be spending about as much time at home revising as they spend in school working. That time is valuable. It adds up so much that it is worth spending some of the time in school to ensure that students actually know how to revise so they don’t fall into any bad habits that waste their time.

Here are things we can do as teachers to ensure the time they are spending revising independently is as effective as possible.

Let them know that ACTIVELY revising is going to be far more effective than PASSIVELY revising. Passive revising includes things like reading, highlighting, copying… and is not a great use of their time. Think of an analogy of working out at the gym; if their head isn’t hurting at the end of revision session, they aren’t doing it right.

2. Don’t overload students with resources. Giving them too much at once is not a kindness. This can be overwhelming and less work can end up being done compared to if a smaller, more accessible task was handed out. Keeping revision simple, one online resource, one workbook, one paper at a time can help.

3. Give students model answers instead of mark schemes. Mark schemes are hard to read and interpret. As a department, creating model answer papers with hints or links to online resources (example below uses Sparx codes), will be of much more use than a hard to read mark scheme.

4. Teach students HOW to use a past paper, these are a precious resource and using them well is hard. Make sure they know that simply DOING a past paper is of little benefit if they don’t reflect on their strengths, learn from their mistakes, and act accordingly.

5. Teach students what good and bad revision looks like.

6. Remind students of the importance of sleeping, eating and creating a focused environment. This is all just as important as the task itself.

Any more to add? Please comment below.

Supercharge Your Mini-Whiteboards

5 tips to take your use of mini-whiteboards to the next level

The importance of checking students’ understanding and then responding to it can not be overstated. I’ve written about this before here. I’m yet to visit a highly performing school that doesn’t already know this. I’m also yet to visit one that doesn’t use mini-whiteboards (MWBs) as the main solution to this problem. If these aren’t already a staple in your classroom I would implore you to look into them. If you have a different solution which gives you reliable and near-instant feedback on the learning of every student in your class then I would sincerely love to hear what you are doing. This post looks at 5 different strategies that can be implemented to take your MWB use to the next level across a variety of subjects.

1. Tweak the Variables

This first technique combines some ideas from responsive teaching and variation theory. Once you’ve taught whatever it is you are teaching, write a question up on the board and have students answer it on their MWBs. Make sure all students end up with the right answer on their boards then start to Tweak the Variables. Tell students not to erase the answer. Then, in front of the students alter one small part of the question and ask students the following “by changing the least possible amount on your board, make it the correct answer to this new question”.

Not only does it give students the chance to exercise their efficiency (laziness?), it can really highlight to students what changes and what stays the same depending on the input.

Examples

Maths – Expand: 2(x+4) –> 2(x-4)–>2(3x-4)–>2x(3x-4)…

Languages – Translate: I eat–> You eat –> You swim –> We swim…

It’s important to end the sequence at some point, have students clean their boards completely and start again from scratch to ensure they can still do the full process. I speak about this in more detail with Craig Barton here.

2. Be Diagnostic

The last thing you want when using MWBs is to ask a question, be presented with a bunch of wrong answers or blank boards and not know what the gap is. Before asking anything that involves multiple steps or concepts check each one individually. These will inevitably be more basic questions than what you are building up to but if it gives students a chance to be successful, that’s no bad thing. Importantly though, if you build a question from the ground up and a student gives the wrong answer you know exactly what you need to do to intervene.

Examples

English: Write down a 2 word imperative sentence–> Identify an imperative in the poem which suggests the writer feels misjudged

Maths: Instead of asking students to complete a Pythagoras’ Theorem question, even once you’ve modelled it, check they can do the individual steps needed.

3. Think Write Pair Rewrite Share (TWPRS)

Chances are you’ve heard of Think Pair Share and probably Think Write Pair Share. By moving this onto MWBs and including a “rewrite” phrase there is a chance for students to take the discussions they have had in their pairs and improve their answers. Whilst this is what is supposed to happen during the “pair” part, the time for students to pause and reflect and then actually make the changes on their initial answer rarely happens. Adding this phase in allows for that to happen and adds an extra layer of accountability before thoughts are shared.

Examples: Anything you would use Think (Write) Pair Share with.

4. Mimic the Task

There is an invisible gap that exists in classrooms sometimes that can completely derail a lesson. It is the gap between what the questions looks like when the class are learning and what the questions looks like when the class are practising. I have seen too many lessons thrown into confusion not because a concept hasn’t been taught well-enough but because the format of the independent task is unfamiliar.

Luckily there is a quick fix, make sure that whatever format the questions start off as match the final questions you ask students as a class on their MWBs. It’s OK (and probably essential most lessons) for questions to deviate from this and more challenge to be introduced down the line. For the students’ sake though, make it a smooth transition and mimic the task as closely as you can before students are set off to work by themselves.

5. Engage then Expand

If the plan is to get students to give a longer and wordier answer than would be appropriate for a MWB then you will probably be best off using cold-call. That’s not to say that MWBs can’t enhance this experience though. Getting students to “dip their toes” into the water of the question with, for example, a quick multiple-choice question can increase engagement. Having all students commit to the beginning of the question before getting individuals to go deeper helps increase the amount of thinking happening in the room.

Examples:

Drama – In the scene we just watched, which had the biggest impact in creating tension A/B/C/D? Boards up. Tommy – why did you choose B? Asmah – you chose C, that’s equally valid, can you explain why?…

Anything you would use cold-calling for.

END

Best of luck trying these out. Let me know how it goes and if you have any other tips to supercharge MWBs.

Starting Strong

Some tips on how to plan and deliver that first lesson. Most likely appropriate for settings where great behaviour and compliance is not a guarantee.

Chipping Norton

When I was on my PGCE we would share horror stories with each other most Friday evenings. This was great fun and often very cathartic. There was an issue though. My first placement school was in Chipping Norton, a quaint market town in rural Oxfordshire. This was David Cameron’s constituency and he had opened their new science block. The school was a stone’s throw away from Jeremy Clarkson’s and Alex James’ houses (the latter would drop in to help the Y9 music students with their Britpop coursework). If you’ve built up a picture of what the students in this school are like, you’d be correct. As a place to hone the craft of teaching without worrying about behaviour, it was a trainee’s dream. The majority of other people on my PGCE were not in the same situation.

Once, in one of our Friday evening moan-fests, I joined in and mentioned how I had a student open a door for me, but in quite a sarcastic manner. Suffice to say, this did not go down well with other trainees who had been verbally abused, had someone start a fire in their classroom, and those that had been physically intimidated. Still, if you’d seen the smirk that kid had on his face when he opened the door for me, I think you’d understand.

I mention the above because I want to give some advice about how to start that first lesson in the academic year with a new class. This advice, I think, mostly holds for the sorts of schools I did not train in but have then spent the majority of my career working at. If these tips don’t seem necessary for you that’s not a problem. They are tips I’ve picked up, the hard way, that have helped me over time. If even one helps you too, that’s enough for me.

Before the First Lesson

Decide the routines you want – Do not start your first lesson coming up with some sort of agreed behavioural charter. There are a lot of students in that room that will need clear rules and leadership. Decide what your expectations are in advance. What routines do you want your students to learn? What ways of working do you want them to have for different phases of your lesson? Decide on these and plan to communicate them, explicitly, with your students from day 1.
Learn the policy – This one is particularly relevant if it is a new school for you. Speak to an experienced teacher and ask them what language the students are used to hearing from their teacher when it comes to using the behaviour policy. Are there verbal warnings, 3 strikes and your out, some sort of C1, C2, C3 system…. Whatever it is, use it, and the language associated with it confidently from day 1. It lets the students know you understand the systems in place. Do not make your own rules that go above, beyond or sideways to the school’s policy. This isn’t fair on the students and (fingers crossed) shouldn’t be needed.
Content not a barrier – Plan lessons where the content is definitely not going to be a barrier to success. If this means pausing how ambitious the curriculum is temporarily, then so be it. It will be worth it in the long run and you need to be sure in the lesson that students are able to access the content you put in front of them as you establish the routines and culture you want. If some complain, let them know it will get more challenging over time as you get to know them better.
Start tight and loosen later – Do not plan any outlandish lessons to begin with. Keep them routine and allow the challenge and intrigue to come from the content. Group tasks, talk tasks, lessons outside… can all wait until you have sorted out the basics.
Make a Seating Plan – Let them know exactly where they will be sitting and stick to that initially. It will most likely be the first time a student challenges a decision you have made. If you can, check with a head of year that the plan is sensible but stick to it for that first lesson. Changes can be made at the start of the next lesson if needed but hold the line publicly with them all.

During the Lesson

Learn their names – Have that seating plan to hand throughout the lesson and learn and use their names as much as possible. If there are pictures on your school’s data system then try to find them and put some faces to names in advance as well just to freak them out a little. It will mostly likely be the case that you end up learning where students sit before you learn who they actually are. I would get students to pack up early and move seats at the end of each lesson. They could only go if I got their name right. This meant I knew them and not just where they sat. This would continue until I would confidently get 100% correct every time. Letting students know that you want to know their names and that whilst they have about 10 new teacher’s names to learn, that you have hundreds of new students makes them sympathetic to the situation.
Rehearse the routines – Have students rehearse the routines you want them to use. If you want a 5-minute silent starter then have 10 ready in advance and have students practise it until they get it right. It may make the first few lessons a slog but it’ll pay dividends in the long run. If you let one student talk in that first lesson, you are giving permission for them all the talk in the next one.
Praise – Relax (or at least appear relaxed on the surface) and give students plenty of praise where it is earned. Not smiling until Christmas is an archaic notion you may come across. In a school with supportive behaviour management systems you should be able to be yourself and trust that the system has your back. Make students feel comfortable and let them know that their hard work will be rewarded.
Firm but fair from day 1 – Do not make any special allowances because it’s the start of the year. Set out your stool early and do so clearly. Sanctions, where earned, will help students know where the line is. It is much easier to loosen rules later (though be sure of your rationale for doing so) than it is to tighten any.

After the Lesson

Phone Home – Phone home for students with a (rough) 3:1 ratio of positive to corrective messages. This is likely not sustainable in the long run but only needs to happen for the first week or so.
Over-Mark their work – This is not sustainable in the long run either, but having eyes on students work initially and writing comments and picking up on issues early on is a great way of preventing them from arising further down the line. Give them your most attentive self for the first 2 weeks then ease off into a more sustainable way of working afterwards.
Catch up Individually – Meet students on an individual basis, with a head of year or form tutor if necessary, that did not act how you wanted and spell out very clearly, what you expect to see of them next time and how sure you are that they can rise to the expectations you are setting for them.

There are a few more tips focused on behaviour which may be useful here.

If you have any more to add then please do so in the comments.

Best of luck with the start of your year!

Teaching Problem Solving (Kind Of)

Students don’t get better at problem solving by simply solving more problems. This is a look at what sorts of problems need solving in school mathematics and some explicit strategies that can help make our students better at it.

This weekend I had the pleasure of talking at my first #MathsConf. I spoke about how I approach teaching students how to become better problem solvers. This is a breakdown of that talk and includes the PowerPoint that was used at the end for download. This topic definitely warrants further exploration in the future but here is most of what was discussed.

Defining Problem Solving

It’s vital that we define problem solving if we’re going to talk about problem solving strategies.

There are many different types of problems that need overcoming. These vary from solving the climate crisis, how to organise one’s time to produce the perfect Christmas dinner, solving Fermat’s Last Theorem to counting how many squares there are in a diagram.

These are undeniably problems that need solving and may have strategies that are useful to employ when attempting to answer them. They do not, however, represent the sort of problem solving students need to perform well in a KS2-KS5 terminal exam. Luckily, the National Curriculum defines exactly the sorts of skills that are needed.

Unfortunately though, these are about as open to interpretation as sentences go. At KS4 these are referred to as AO3 (Assessment Objective 3). It is possible to search on an exam board’s bank of questions for where this objective has been assessed in the past. Doing so yields examples like these:

Some, like the nested triangles and multi-step circle theorem questions, may look familiar and people are sometimes surprised to know that these even count as “problem solving” questions. That’s good news though. It shows that the types of questions that assess a student’s ability to problem solve can be quite narrow and predictable. Because of that, it makes the skills needed to succeed with them teachable.

There will be students that can access these questions without any extra help. That can make it tempting to assume all students should be able to do this. This is not the case however and, much like it would be our job to fix any gaps in a student’s times tables knowledge for example, it is also our job to equip them with any skills they are missing out on compared to their peers. If we ever want to close the attainment gap in this country we need to ensure that all the implicit skills the more advantaged students have are distilled and taught to the others.

The Goldilocks Zone

So what are these skills? Well, they need to be specific enough to be explicitly taught. They also need to be generic enough to be useful in a variety of situations. They need to be “just right”.

There are a few labelled in the diagram, some may look familiar, others should not (I made them up). I will discuss “Zoom In – Zoom Out” and “Number-Free Problems” below. But first…

Embedding Problem Solving into the Curriculum

These strategies, once distilled, need to be interleaved throughout the curriculum. They need to be introduced at an appropriate stage and then included in any retrieval activities, codified and shared across a department, and referred to throughout a student’s time in their school. They are not to be left until the last 2 weeks of Year 11, nor are they something to be talked about once and then forgotten. That doesn’t work for teaching anything else and it won’t work for this either.

The Strategies

Number-Free Problems

The first idea is to encourage students to ignore the numbers when they first read a question.

I’d argue that most people fluent with the idea of area, proportion, and substitution would confidently be able to say they can solve these questions. There’s obviously an important factor missing here, but the numbers are not a crucial part of the formulation of the problem, just of the almost arbitrary calculating of the solution.

The human brain can hold about 7 things in its working memory at any one time. If you focus on the surface details, in this case the numbers, then you are taking up valuable space. It doesn’t matter so much with the low-complexity level of the questions above but what about this one:

Trying to solve this, whilst caring about the 10 numbers on show is very tricky. Ignore the numbers of this “problem solving” question however and, I think, it becomes easier. My argument is that those students who successfully answer questions like this are already doing this strategy. We just need to make the implicit explicit. It forces students to engage with the deep structure of the problem to produce a plan like below:

They cannot get carried away with the numbers and just randomly try adding or multiplying the first few values they see. Here it is with another problem:

These are KS4 questions but this strategy can be applicable to KS2-KS5 content. Equipping students with the strategy of ignoring the numbers and producing a written plan for those big mark questions feels like a positive step towards closing the gap. Teaching this to students early on and referring to the strategy throughout their schooling could be immensely powerful.

Zoom In – Zoom Out

This strategy is more suitable to geometry questions. Again, I think this is something a lot of people do automatically, and its something we should be explicitly teaching all students.

The idea is to ignore certain parts of a diagram at any one time and focus in on what it is that’s needed. If asked to find x in the diagram below it could be overwhelming.

Once you’ve isolate the 2 lines that make x and the other parallel line though you are left with:

I think this is the sort of mental “zooming in and zooming out” that successful problem solvers are doing. Making this clear to students and giving them time to practice it feels purposeful.

Making it clear with this question:

That it is useful to either mentally or physically have this image in your head:

In Summary

I think there are a set of explicit, teachable, skills we can pass onto students in order for them to better access the AO3 or “problem solving” marks available to them. This involves distilling the things that experts do implicitly, automatically, and turning them into named strategies that are embedded throughout a curriculum.

My thanks to you for reading this, to MathsConf for letting me talk about this, and to the audience for choosing and then engaging with the session. Please find the PPT that was used for the session below.

problem-solving Download

I also spoke about this for Tip#1 in Craig Barton’s Tips for Teachers podcast if you want to hear parts of it again (along with 4 other topics) https://tipsforteachers.co.uk/craig-latimir/